In the last post I showed how to calculate the Julian Day (JD) and the Ephemeris Time (T). Now I want to build on that to calculate the geocentric (or apparent) coordinates of the Sun for any given moment in time. This algorithm is taken from Astronomical Algorithms by Jean Meeus (2nd Edition) with modifications from the U.S. Naval Observatory. All page number references are to Meeus’ book.
The goal here is to input any date and time (say the launch of Sputnik 1 on 4 Oct 1957 at 19:29 UTC) and get back the coordinates of the Sun as it appears to us on the celestial sphere at that moment. I recommend reading an introductory article Position of the Sun before continuing. For the complete software solution implemented in C# see my GitHub repo. Note that you will need to download and install the free Microsoft Visual Studio Community Edition 2017 to build and run the code.
Introduction
Sputnik 1 launched at 1957-10-04T19:29:00Z. From the previous post that gives us a T value of -0.42241. See my Moment.cs struct in the source code for the calculations. This value is going to be used in most every function below.
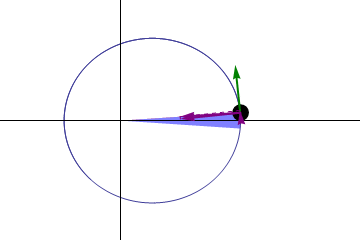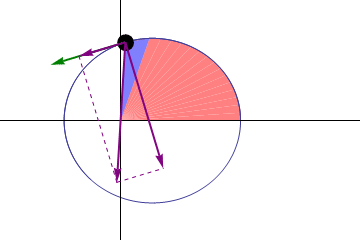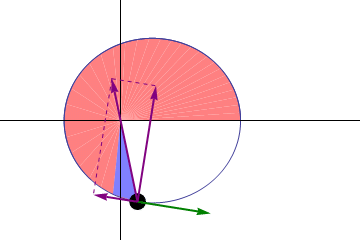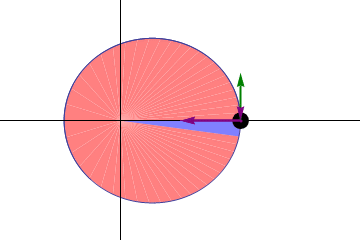
I want to say a few things about planetary motion to provide context. There are two important angles with which we will be working. The first is called the mean anomaly and the second is the true anomaly. When calculating either one we start with an orbiting body at perihilion and the angle is zero degrees. Notice the starting position in this figure:

The angle increases as the body moves in its orbit so that if it goes all the way around once it is 360 degrees. Because we’re dealing with long time spans (and multiple orbits) we will be dealing with very large angles. I’ll show how these are converted to between 0 and 360 degrees. Also, like many programming languages, C# requires arguments passed into trigonometric functions to be in radians. So there will be conversions between degrees and radians.
Johannes Kepler discovered that the shape of a planet’s orbit around the Sun is an ellipse. This is his First Law. Kepler’s Second Law states that planets sweep out equal areas in equal times so that they move faster when at perihelion (closer to the sun) and slower when at aphelion (further from the Sun). This animation illustrates this effect:
Notice the “pie slices” have greater interior angles at perihelion than they do at aphelion due to the varying angular velocity of the orbiting body. Notice also the angle described by the orbiting body and the focal point around which it orbits (in light red). This angle is the true anomaly of the orbiting body. We will calculate the mean anomaly first and then convert that to true anomaly later.
We will do the same thing with the Sun’s longitude, first calculating the mean longitude and then using that later to find the true longitude. So here are exact steps which I will follow to arrive at the solar coordinates for a given moment in time:
- Calculate the geometric mean longitude L0 of the Sun referred to the mean equinox of the time T.
- Calculate the mean anomaly M of the Sun at time T.
- Calculate the eccentricity e of the Earth’s orbit at time T.
- Using the mean anomaly M from Step 2 calculate the Sun’s equation of the center C at time T.
- Given Steps 1 through 4 calculate the Sun’s true longitude and true anomaly.
- Calculate the Sun’s radius vector R (the heliocentric distance from the Sun to the Earth center-to-center).
- Correct for nutation and aberration in order to get the Sun’s apparent longitude referred to the true equinox of time T.
- Calculate the obliquity of the ecliptic (the inclination of the Earth’s equator with respect to the plane at which the Sun and planets appear to move across the sky).
- Finally by this step we have all the information we need to obtain the apparent position of the Sun on the celestial sphere at time T.
I realize there’s a lot of technical terms in there. So let’s take this one step at a time.
Step 1: Geometric Mean Longitude of the Sun
Suppose you wanted to know the exact position of a geocache buried somewhere on Earth. Well you just use your GPS and go find it right? But suppose the geocache was buried 10,000 years ago? Or 160,000 years ago? Because of plate tectonics the continents have drifted in fits and starts over the intervening centuries. If enough time goes by you’d find that you were digging in the wrong place.
When dealing with planetary motion astronomers face a similar problem. Movements are not easily predictable because as I mentioned earlier planets move in a nonuniform way (anomalously). For example, the Earth is tugged and pulled by the Moon’s gravity. It also wobbles on its axis due to an effect called precession. So we need a way to reference where the Sun, planets, and celestial markers (like the First Point of Aries) line up with the Earth at a given point in time. Our calculations can then be referenced to that moment. In astronomy this is called equinox of date:
Because of the precession of the Earth’s axis, the position of the vernal point on the celestial sphere changes over time, and the equatorial and the ecliptic coordinate systems change accordingly. Thus when specifying celestial coordinates for an object, one has to specify at what time the vernal point and the celestial equator are taken. That reference time is called the equinox of date. [Montenbruck, Oliver; Pfleger, Thomas. Astronomy on the Personal Computer. Springer-Verlag. p. 17 spotted on Wikipedia]
When our calculations reference a particular time frame we call this frame of reference an epoch. Currently we use the J2000.0 epoch. This epoch started on 1 Jan 2000 at noon UTC. At that exact moment the mean longitude of the Sun was at:
280° 27′ 59.26″ (or 280.46646 decimal degrees)
So Step 1 is all about finding where the mean Sun was at time T referred to the equinox of date. To do that we have to start with the Sun’s mean longitude at J2000.0 above and calculate backward or forward for dates prior to or later than the current epoch. That is to say our formula is going to be epoch +/- time T with some corrections for perturbations that Meeus adds:
double L0 = 280.46646 + (36000.76983 * T) + (0.0003032 * Math.Pow(T, 2)); L0 = L0.CorrectDegreeRange(); // extensions to C# type double
Because planetary orbit calculations generate very large angles we need to reduce such angles to between 0 and 360 degrees. I have a small static class in the project called DoubleExtensions.cs where I’ve extended the C# double type with the CorrectDegreeRange function used above. I’ll use this extension method with other such large angles.
/// <summary>
/// For very large angles correct to put between 0 and 360 degrees
/// </summary>
/// <param name="d"></param>
/// <returns></returns>
public static double CorrectDegreeRange(this double d)
{
d = d % 360;
if (d < 0)
{
d += 360;
}
return d;
}
Step 2: Mean Anomaly of the Sun
As I said in the introduction, the word “anomaly” here refers to the nonuniform or “anomalous” apparent motion of the Sun and planets along the plane of the ecliptic. Meeus defines the mean anomaly as “the angular distance from perihelion which the [Earth] would have if it moved around the Sun with a constant angular velocity” (p. 194). I should say that the word “apparent” is always used to denote that the Sun, planets, and stars appear to move across the sky in a 24-hour period. Obviously, the true movement is the rotation of the Earth on its axis but it is convenient to speak of the apparent motion of the Sun and planets across the sky.
The mean anomaly M of the Sun can be calculated as:
// mean anomaly of the Sun (25.3) double M = 357.52911 + (35999.05029 * T) - (0.0001537 * Math.Pow(T, 2)); M = M.CorrectDegreeRange();
Notice on line 3 I’m again correcting a very large angle to put it between 0 and 360 degrees.
Step 3: Eccentricity of the Earth’s Orbit
The eccentricity refers to the “flatness” of the ellipse swept out by the Earth in it orbit around the Sun. In this illustration there is increasing eccentricity from top to bottom where the first image is a circle and the bottom ellipse is highly eccentric:
Eccentricity e of the Earth’s orbit is a very small value. To calculate it:
// eccentricity of Earth's orbit (25.4) double e = 0.016708634 - (0.000042037 * T) - (0.0000001267 * Math.Pow(T, 2));
The initial constant 0.01670834 is barely modified by the tiny corrections in the rest of the equation. If time T is the 1957 Sputnik launch then e == 0.01672. Earth’s orbit tends to be closer to a circle than to a very flat ellipse. So that’s why this is a small value. (Periodic comets on the other hand can have highly eccentric orbits in which they spend decades moving slowly through the icy regions of the outer solar system only to whip around the sun in a matter of a few weeks.)
Step 4: Equation of the Center
There is a Wikipedia article on the equation of the center and I’ll just warn you now it is a tough slog. If you’re like me you have to read it more than once. Here’s the general idea on what we need to do here: we need to get the Sun’s true anomaly n (Step 5 below). But before we can do that we need to solve something called Kepler’s Equation. That is a huge topic and I’m not going into it here. I’ll just say that per Meeus (Chapter 30) we can get away with calculating the equation of the center instead of solving Kepler’s equation. This is possible because the Earth’s orbital eccentricity e is so small. (As calculated above Earth’s orbit is a case where 0 < e < 1 and e = 0.01672.)
So the following calculation is an accurate enough approximation for our purposes. Here’s the calculation for determining the Sun’s equation of center:
// Sun's equation of center
double C =
+(1.914602 - (0.004817 * T) - (0.000014 * Math.Pow(T, 2))) * Math.Sin(M.ToRadians())
+ (0.019993 - (0.000101 * T)) * Math.Sin(M.ToRadians() * 2)
+ (0.000289 * Math.Sin(M.ToRadians() * 3));
Step 5: True Longitude and True Anomaly
We calculated the mean longitude and mean anomaly back in Steps 1 and 2. With the equation of center C we are now ready to calculate the true (geometric) longitude and true anomaly:
// Sun's true geometric longitude double Ltrue = (L0 + C); Ltrue = Ltrue.CorrectDegreeRange(); // Sun's true anomaly double n = (M + C); n = n.CorrectDegreeRange();
It’s traditional to use the Greek letter ν (nu) as the true anomaly. But in the source code I’m using the English letter n.
Step 6: Calculate the Radius Vector
Next we need to calculate the radius vector R, which is the distance (measured in astronomical units or AU) between the center of the Sun and the center of the Earth. Meeus’ formula provides a value slightly greater than 1 even though his example in figure 25a (p. 165) shows a value less than 1 (0.997). So instead I’ll follow an algorithm from the U.S. Naval Observatory (USNO):
// U.S. Naval Observatory function for radius vector.
// Compare to Meeus (25.5)
double R = 1.00014
- 0.01671 * Math.Cos(M.ToRadians())
- 0.00014 * Math.Cos(2 * M.ToRadians());
Step 7: The Apparent Longitude of the Sun
This is an optional step. We could calculate the solar coordinates using true longitude. But this step provides greater accuracy so I’ll include it. Essentially we need to calculate a value called Ω (“omega” or O) that corrects the Sun’s true longitude for perturbations (like the Moon’s tidal force on the Earth). So we calculate O and then use that to get the apparent longitude:
// correction "omega" for nutation and aberration double O = 125.04 - (1934.136 * T); // apparent longitude L (lambda) of the Sun double Lapp = Ltrue - 0.00569 - (0.00478 * Math.Sin(O.ToRadians()));
Step 8: Obliquity of the Ecliptic
The obliquity is an effect caused by the tilt of the Earth on its axis with respect to the celestial equator. In other words, it is the angle between the plane of the Earth’s equator and the plane across which the Sun and planets appear to travel. The calculation for this is Meeus’ high-accuracy version:
// obliquity of the ecliptic (22.2)
double U = T / 100;
double e0 =
new Angle(23, 26, 21.448).Degrees
- new Angle(0, 0, 4680.93).Degrees * U
- 1.55 * Math.Pow(U, 2)
+ 1999.25 * Math.Pow(U, 3)
- 51.38 * Math.Pow(U, 4)
- 249.67 * Math.Pow(U, 5)
- 39.05 * Math.Pow(U, 6)
+ 7.12 * Math.Pow(U, 7)
+ 27.87 * Math.Pow(U, 8)
+ 5.79 * Math.Pow(U, 9)
+ 2.45 * Math.Pow(U, 10);
In my source code on GitHub there is an Angle struct that is convenient for initializing an angle from known degrees, arc minutes, and arc seconds. I can also convert between degrees and radians as the need arises.
Step 9: Solar Coordinates
At last we can calculate right ascension a and declination d of the apparent position of the Sun on the celestial sphere at time T. We’re going to correct e for parallax and feed the corrected value into the two main functions:
// correction for parallax (25.8)
double eCorrected = e0 + 0.00256 * Math.Cos(O.ToRadians());
// Sun's right ascension a
double a = Math.Atan2(
Math.Cos(eCorrected.ToRadians()) * Math.Sin(Lapp.ToRadians()),
Math.Cos(Lapp.ToRadians()));
// declination d
double d = Math.Asin(Math.Sin(eCorrected.ToRadians()) * Math.Sin(Lapp.ToRadians()));
// solar coordinates
RightAscension ra = new RightAscension(a.ToDegrees());
Angle dec = new Angle(d.ToDegrees());
If I run the whole program I get these solar coordinates:

These coordinates are center-to-center with respect to the equator. (Sputnik 1 was launched at 22:29 Moscow local time). If you cloned my GitHub repo to your laptop you can plug in other dates of your choosing. Five test dates and times are already configured as project properties. In addition to the Sputnik 1 launch date there are the two upcoming solstices and two equinoxes for 2019:

Conclusion
You can see the algorithm is accurate to within a second for right ascension and well within one arc minute for declination. Please contact me or leave a comment if you find an error in this post! I’ll correct it as soon as possible. Also, leave a comment if you have an interest in this sort of thing and would like to see other implementations. Positions of the four main moons of Jupiter at a given date and time? Lunar or solar eclipses? Let me know!